HAVO 4 Hoofdstuk 7: Allerlei formules

Evenredigheid
a = evenredigheidsconstante
Let op! Geef het verschil tussen A en a duidelijk aan!

Recht evenredig
y is recht evenredig met x Formule: y = ax a berekenen: a = y/x	A is recht evenredig met s Formule: A = as a berekenen: a = A/s	N is recht evenredig met d3 Formule: N = a * d3 a berekenen: a = N/d3	Q is recht evenredig met p0,67 Formule: Q = a * p0,67 a berekenen: a = Q/p0,67

Omgekeerd evenredig
y is omgekeerd evenredig met x Formule: y = a/x a berekenen: a = xy	C is omgekeerd evenredig met h Formule: C = a/h a berekenen: a = Ch	y is omgekeerd evenredig met x5 Formule: y = a/x5 a berekenen: a = y * x5	M is omgekeerd evenredig met l-0,37 Formule: M = a/l-0,37 a berekenen: a = M * l-0,37

Evenredigheid aantonen in een tabel
Is y recht evenredig met x?
y/x bij minstens 5 getallen proberen (niet alleen de eerste 5 of alleen de laatste 5, maar getallen uit zowel het begin, als het midden en het eind van de tabel nemen!)
Komt er steeds hetzelfde getal uit? Dat getal is a, de evenredigheidsconstante. Formule: y = ax
Komt er steeds een ander getal uit? Dan zijn y en x NIET recht evenredig.

Is y³ recht evenredig met x⁵?
y³/x⁵ bij minstens 5 getallen proberen (niet alleen de eerste 5 of alleen de laatste 5, maar getallen uit zowel het begin, als het midden en het eind van de tabel nemen!)
Komt er steeds hetzelfde getal uit? Dat getal is a, de evenredigheidsconstante. Formule: y³ = ax⁵
Komt er steeds een ander getal uit? Dan zijn y³ en x⁵ NIET recht evenredig.


Is y omgekeerd evenredig met x?
y * x bij minstens 5 getallen proberen (niet alleen de eerste 5 of alleen de laatste 5, maar getallen uit zowel het begin, als het midden en het eind van de tabel nemen!)
Komt er steeds hetzelfde getal uit? Dat getal is a, de evenredigheidsconstante. Formule: y = a/x
Komt er steeds een ander getal uit? Dan zijn y en x NIET omgekeerd evenredig.

Is y^0,66 omgekeerd evenredig met x^2.59?
y^0,66 * x^2.59 bij minstens 5 getallen proberen (niet alleen de eerste 5 of alleen de laatste 5, maar getallen uit zowel het begin, als het midden en het eind van de tabel nemen!)
Komt er steeds hetzelfde getal uit? Dat getal is a, de evenredigheidsconstante. Formule: y^0,66 = a/x^2.59
Komt er steeds een ander getal uit? Dan zijn y^0,66 en x^2.59 NIET omgekeerd evenredig.



y = a/x + b

Horizontale assymptoot (H.A.): Grote getallen voor x invullen. (Let op! Niet vergeten "y =" op te schrijven!)
Verticale assymptoot (V.A.): Je mag niet delen door 0! Dat geeft een assymptoot. (Let op! Niet vergeten "x =" op te schrijven!)

Assymptoten vinden
y = 200/x + 5 H.A.: y = 5 V.A.: x = 0	y = 36/x - 8,66 H.A.: y = -8,66 V.A.: x = 0	y = -6 + 88,9/x H.A.: y = -6 V.A.: x = 0	y = 66/(x + 4) + 2 H.A.: y = 2 V.A.: x + 4 = 0 dus x = -4

Machtsfuncties
y = axⁿ
Plaatjes gelden voor n > 1

n even		n oneven
a positief	a negatief	a positief	a negatief

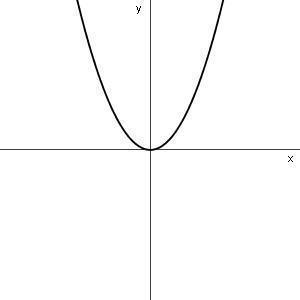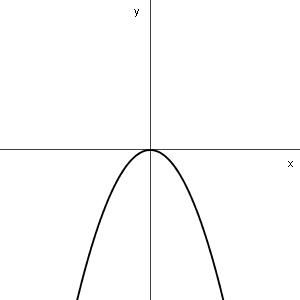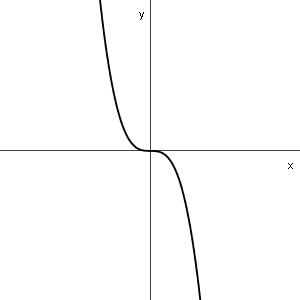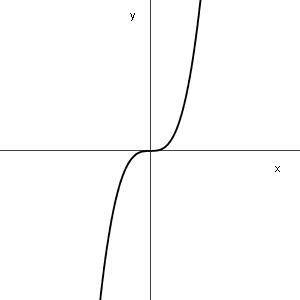Machtsfuncties oplossen
y = axⁿ
Als je y niet weet: getallen invullen
Als je a niet weet: a = y/(xⁿ)
Als je x niet weet: GR: intersect
Als je n niet weet: GR: intersect



Rekenhulpje
6/3 = 2
6/2 = 3
6 = 3 * 2