5VWO Hoofdstuk 8: Normale verdeling
Voorkennis
Frequentieverdeling (waarnemingsgetallen, frequenties)
Frequentiepolygoon (geen vloeiende lijn, getallen boven het klassemidden)
Relatieve frequentieverdeling (percentages)
Relatief frequentiepolygoon (geen vloeiende lijn, percentages boven het klassemidden)
Cumulatieve frequentieverdeling (frequenties optellen)
Cumulatief frequentiepolygoon (geen vloeiende lijn, getallen boven de rechtergrens)
Relatief cumulatieve frequentieverdeling (precentages optellen)
Relatief cumulatief frequentiepolygoon (geen vloeiende lijn, percentages boven de rechtergrens)
Centrummaten
Boxplot
Om een boxplot te tekenen heb je 5 waarden nodig: kleinste getal, eerste kwartiel (Q1), mediaan, derde kwartiel (Q3), grootste getal. De tekening (boven een getallenlijn) komt er als volgt uit te zien:
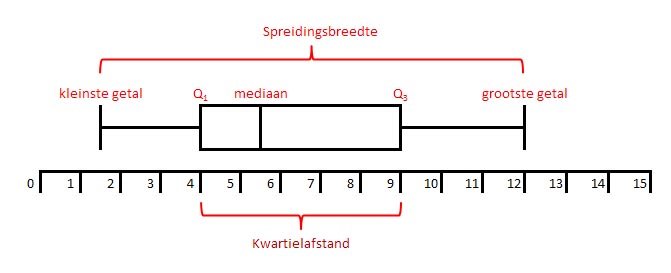
De afstand tussen het grootste en het kleinste getal heet de spreidingsbreedte, de afstand tussen Q1 en Q3 heet de kwartielafstand.
Standaarddeviatie/Standaardafwijking
De standaarddeviatie of standaardafwijking is de gemiddelde afstand van het gemiddelde.
1. Bereken het gemiddelde.
2. Maak een tabel met bovenaan alle getallen.
3. Zet in je gemaakte tabel, onder elk cijfer, de afwijking van het gemiddelde, d (ook wel deviatie genoemd).
4. Zet de regel eronder alle d2.
5. Tel alle d2 bij elkaar op.
6. Deel door het aantal gebruikte getallen.
7. Neem de wortel.
Centrummaten en boxplot met de GR
Maak een frequentietabel (links alle waargenomen getallen, rechts de frequentie van die waargenomen getallen).
Ga naar STAT → EDIT → 1: Edit...
Neem de tabel over in List1 (linkerkant van de tabel, waarnemingen) en List2 (rechterkant van de tabel, frequenties).
Om de centrummaten te berekenen ga je weer naar je hoofdmenu (2nd → MODE). Daar typ je in:
STAT → CALC → 1: 1-VAR Stats → ENTER → 2nd → 1 → , → 2nd → 2 → ENTER
Vuistregels voor de normale verdeling
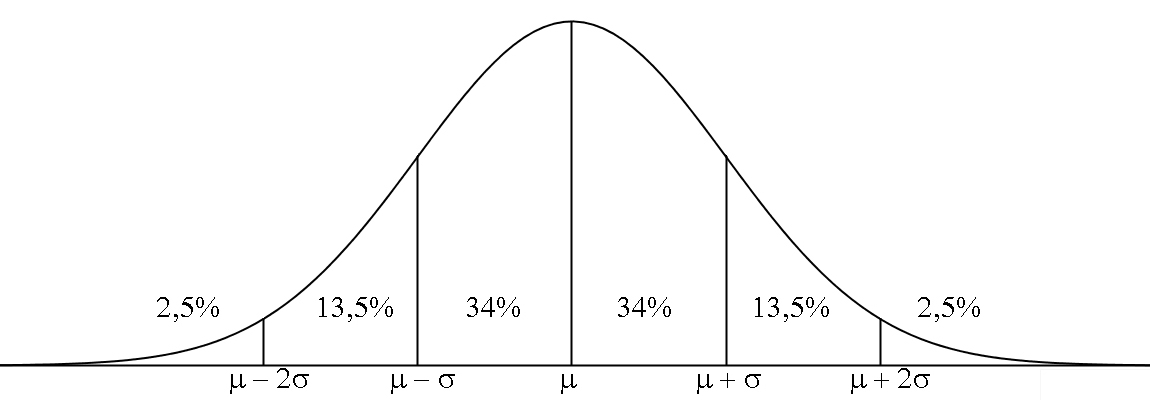
De onderstaande normaalkromme met alle bijbehorende getallen moet je UIT JE HOOFD kunnen tekenen.
Normale verdeling met de grafische rekenmachine
Onthoud goed:
De oppervlakte onder de hele kromme is altijd 1
De kromme is symmetrisch (je kan hem spiegelen in de lijn ¨¬)
2ND → VARS → 3:invNorm(
2ND → VARS → 2:normalcdf(
Bij alle vragen over een normale verdeling waar de bijbehorende kromme niet gegeven is, moet je hem ZELF tekenen.
1) Normaalkromme tekenen
2) Streep zetten bij de linker- en/of rechtergrens
3) De oppervlakte die je hebt gekregen of moet uitrekenen, inkleuren of arceren
4) Rechtsboven de normaalkromme zetten: µ, σ en opp.
Grens uitrekenen:
invNorm(oppervlakte LINKS naast grens, µ, σ) = grens
Grenzen altijd afronden op 1 decimaal meer dan de gegeven σ, tenzij anders vermeld in de vraag.
Oppervlakte uitrekenen:
normalcdf(linkergrens, rechtergrens, µ, σ) = oppervlakte
µ uitrekenen:
Y1 = normalcdf(linkergrens, rechtergrens, X, σ)
Y2 = oppervlakte
Optie intersect geeft x = ... en y = ...
Dus: µ = ... (de waarde die je voor x hebt gevonden)
OF
Y1 = invNorm(oppervlakte LINKS naast grens, X, σ)
Y2 = grens
Optie intersect geeft x = ... en y = ...
Dus: µ = ... (de waarde die je voor x hebt gevonden)
σ uitrekenen:
Y1 = normalcdf(linkergrens, rechtergrens, µ, X)
Y2 = oppervlakte
Optie intersect geeft x = ... en y = ...
Dus: σ = ... (de waarde die je voor x hebt gevonden)
OF
Y1 = invNorm(oppervlakte LINKS naast grens, µ, X)
Y2 = grens
Optie intersect geeft x = ... en y = ...
Dus: σ = ... (de waarde die je voor x hebt gevonden)
Voorkennis
Frequentieverdeling (waarnemingsgetallen, frequenties)
Frequentiepolygoon (geen vloeiende lijn, getallen boven het klassemidden)
Relatieve frequentieverdeling (percentages)
Relatief frequentiepolygoon (geen vloeiende lijn, percentages boven het klassemidden)
Cumulatieve frequentieverdeling (frequenties optellen)
Cumulatief frequentiepolygoon (geen vloeiende lijn, getallen boven de rechtergrens)
Relatief cumulatieve frequentieverdeling (precentages optellen)
Relatief cumulatief frequentiepolygoon (geen vloeiende lijn, percentages boven de rechtergrens)
Centrummaten
| Modus | Degene die het meeste voorkomt. Is niet altijd aanwezig. De enige centrummaat die je voor kwantitatieve gegevens (gegevens zonder cijfers, zoals de kleur van schoenen) kan gebruiken. |
| Mediaan | Middelste getal als je alle getallen van klein naar groot opschrijft. Niet gevoelig voor uitschieters. |
| Gemiddelde | Alle getallen bij elkaar optellen en delen door het aantal getallen. Gebruikt alle getallen, maar is gevoelig voor uitschieters. |
| Eerste kwartiel (Q1) | Mediaan van alle getallen links van de mediaan. |
| Derde kwartiel (Q3) | Mediaan van alle getallen rechts van de mediaan. |
| Voorbeeld | |
| Bepaal handmatig de modus vande volgende rij getallen: 4 4 7 8.5 11 8.5 4.5 4 1.5 3 12 9.5 4.5 5.5 8.5 9 12 5 11 8.5 4 5.5 4 |
|
| Antwoord | |
| Maak een frequentietabel. | |
| Getal | Frequentie |
| 1.5 | 1 |
| 3 | 1 |
| 4 | 5 |
| 4.5 | 2 |
| 5 | 1 |
| 5.5 | 2 |
| 7 | 1 |
| 8.5 | 4 |
| 9 | 1 |
| 9.5 | 1 |
| 11 | 2 |
| 12 | 2 |
| Je ziet dat de 4 het vaakst voorkomt (namelijk 5 keer). Dus 4 is de modus. | |
Boxplot
Om een boxplot te tekenen heb je 5 waarden nodig: kleinste getal, eerste kwartiel (Q1), mediaan, derde kwartiel (Q3), grootste getal. De tekening (boven een getallenlijn) komt er als volgt uit te zien:

De afstand tussen het grootste en het kleinste getal heet de spreidingsbreedte, de afstand tussen Q1 en Q3 heet de kwartielafstand.
| Voorbeeld |
| Maak handmatig een boxplot bij de volgende rij getallen: 4 4 7 8.5 11 8.5 4.5 4 1.5 3 12 9.5 4.5 5.5 8.5 9 12 5 11 8.5 4 5.5 4 |
| Antwoord |
| Zet alle getallen op een rij van klein naar groot. 1.5 3 4 4 4 4 4 4.5 4.5 5 5.5 5.5 7 8.5 8.5 8.5 8.5 9 9.5 11 11 12 12 Bepaalde vijf benodigde getallen: Kleinste getal: 1,5 Grootste getal: 12 Mediaan: er zijn 23 getallen, de middelste ((23 + 1) / 2 = 12ste) getal is 5,5 Eerste kwartiel (Q1): er staan 11 getallen links van de mediaan, het middelste ((11 + 1) / 2 = 6de) getal is 4. Derde kwartiel (Q3): er staan 11 getallen rechts van de mediaan, het middelste ((11 + 1) / 2 = 6. 6 + 12 = 18de) getal is 9. De bijbehorende tekening is hierboven al gegeven (in het zwart). |
| Voorbeeld |
| Maak handmatig een boxplot bij de volgende rij getallen: 5.5 9.5 12 7 3 1.5 2 4 6.5 8.5 11 9.5 4 4 8.5 4.5 2 9.5 11 12 8.5 4 4 4 6 7 12 2.5 4 4 7 4.5 3 8.5 11 9 5 4 5.5 11 3 6 12 4.5 5.5 8.5 9.5 5 4 5 5.5 11 6 3 4.5 Bereken de spreidingsbreedte en kwartielafstand. |
| Antwoord |
| Zet alle getallen op een rij van klein naar groot. 1.5 2 2 2.5 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4.5 4.5 4.5 4.5 5 5 5 5.5 5.5 5.5 5.5 6 6 6 6.5 7 7 7 8.5 8.5 8.5 8.5 8.5 9 9.5 9.5 9.5 9.5 11 11 11 11 11 12 12 12 12 Bepaalde vijf benodigde getallen: Kleinste getal: 1,5 Grootste getal: 12 Mediaan: er zijn 55 getallen, de middelste ((55 + 1) / 2 = 28ste) getal is 5,5 Eerste kwartiel (Q1): er staan 27 getallen links van de mediaan, het middelste ((27 + 1) / 2 = 14de) getal is 4. Derde kwartiel (Q3): er staan 27 getallen rechts van de mediaan, het middelste ((27 + 1) / 2 = 14. 14 + 28 = 42ste) getal is 9. De bijbehorende tekening is hierboven al gegeven (in het zwart). Spreidingsbreedte: 12 - 1.5 = 10.5. Kwartielafstand: 9 - 4 = 5. |
Standaarddeviatie/Standaardafwijking
De standaarddeviatie of standaardafwijking is de gemiddelde afstand van het gemiddelde.
1. Bereken het gemiddelde.
2. Maak een tabel met bovenaan alle getallen.
3. Zet in je gemaakte tabel, onder elk cijfer, de afwijking van het gemiddelde, d (ook wel deviatie genoemd).
4. Zet de regel eronder alle d2.
5. Tel alle d2 bij elkaar op.
6. Deel door het aantal gebruikte getallen.
7. Neem de wortel.
| Voorbeeld | |||||||||
| In een klas hebben negen leerlingen de volgende cijfers gehaald: 5, 6, 7, 8, 9, 10.Bereken de standaarddeviatie. | |||||||||
| Antwoord | |||||||||
| 1. Gemiddelde: (5 + 6 + 7 + 8 + 9 + 10)/6 = 7.5 | |||||||||
| 2. Getallen | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 3. d | 5 - 7.5 = -2.5 | 6 - 7.5 = -1.5 | 7 - 7.5 = -0.5 | 8 - 7.5 = 0.5 | 9 - 7.5 = 1.5 | 10 - 7.5 = 2.5 | |||
| 4. d2 | (-2.5)2 = 6.25 | (-1.5)2 = 2.25 | (-0.5)2 = 0.25 | 0.52 = 0.25 | 1.52 = 2.25 | 2.52 = 6.25 | |||
|
5. Som van alle d2: (6.25 + 2.25 + 0.25 + 0.25 + 2.25 + 6.25) = 17.5 6. Delen door totaal aantal getallen: 17.5/6 ≈ 2.917. 7. Worteltrekken: √(2.917) ≈ 1.708. |
|||||||||
| Voorbeeld | |||||||||
| In een klas hebben negen leerlingen de volgende cijfers gehaald: 1, 4, 5, 5, 6, 8, 8, 8, 9. Bereken de standaarddeviatie. | |||||||||
| Antwoord | |||||||||
| 1. Gemiddelde: (1 + 4 + 5 + 5 + 6 + 8 + 8 + 8 + 9)/9 = 6 | |||||||||
| 2. Getallen | 1 | 4 | 5 | 5 | 6 | 8 | 8 | 8 | 9 |
| 3. d | 1 - 6 = -5 | 4 - 6 = -2 | 5 - 6 = -1 | 5 - 6 = -1 | 6 - 6 = 0 | 8 - 6 = 2 | 8 - 6 = 2 | 8 - 6 = 2 | 9 - 6 = 3 |
| 4. d2 | (-5)2 = 25 | (-2)2 = 4 | (-1)2 = 1 | (-1)2 = 1 | 02 = 0 | 22 = 4 | 22 = 4 | 22 = 4 | 32 = 9 |
|
5. Som van alle d2: (25 + 4 + 1 + 1 + 0 + 4 + 4 + 4 + 9) = 52 6. Delen door totaal aantal getallen: 52/9 ≈ 5,778. 7. Worteltrekken: √(5,7787) ≈ 2,404. |
|||||||||
Centrummaten en boxplot met de GR
Maak een frequentietabel (links alle waargenomen getallen, rechts de frequentie van die waargenomen getallen).
Ga naar STAT → EDIT → 1: Edit...
Neem de tabel over in List1 (linkerkant van de tabel, waarnemingen) en List2 (rechterkant van de tabel, frequenties).
Om de centrummaten te berekenen ga je weer naar je hoofdmenu (2nd → MODE). Daar typ je in:
STAT → CALC → 1: 1-VAR Stats → ENTER → 2nd → 1 → , → 2nd → 2 → ENTER
| Voorbeeld | |
| Bereken het gemiddelde en de standaardafwijking, en maak een boxplot bij de volgende rij getallen: 5.5 9.5 12 7 3 1.5 2 4 6.5 8.5 11 9.5 4 4 8.5 4.5 2 9.5 11 12 8.5 4 4 4 6 7 12 2.5 4 4 7 4.5 3 8.5 11 9 5 4 5.5 11 3 6 12 4.5 5.5 8.5 9.5 5 4 5 5.5 11 6 3 4.5. | |
| Antwoord | |
| Maak een frequentietabel. | |
| Getal | Frequentie |
| 1.5 | 1 |
| 2 | 2 |
| 2.5 | 1 |
| 3 | 4 |
| 4 | 10 |
| 4.5 | 4 |
| 5 | 3 |
| 5.5 | 4 |
| 6 | 3 |
| 6.5 | 1 |
| 7 | 3 |
| 8.5 | 5 |
| 9 | 1 |
| 9.5 | 4 |
| 11 | 5 |
| 12 | 4 |
|
Neem de tabel over in je GR (linkerkolom in List1, rechterkolom in List2 want links zijn waarnemingen en rechts zijn frequenties). GR: 1-Var Stats L1,L2 geeft: Gemiddelde: 6.418 Standaardafwijking: 3.031 Kleinste getal: 1.5 Eerste kwartiel (Q1): 4 Mediaan: 5.5 Derde kwartiel (Q3): 9 Grootste getal: 12 De bijbehorende tekening is hierboven al gegeven (in het zwart). |
|
Vuistregels voor de normale verdeling
De onderstaande normaalkromme met alle bijbehorende getallen moet je UIT JE HOOFD kunnen tekenen.

| Voorbeelden van vragen | ||
|
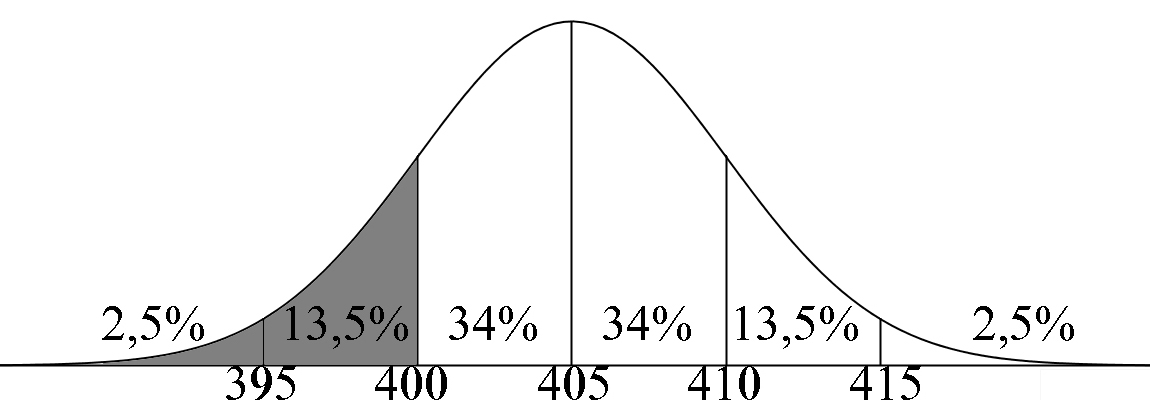
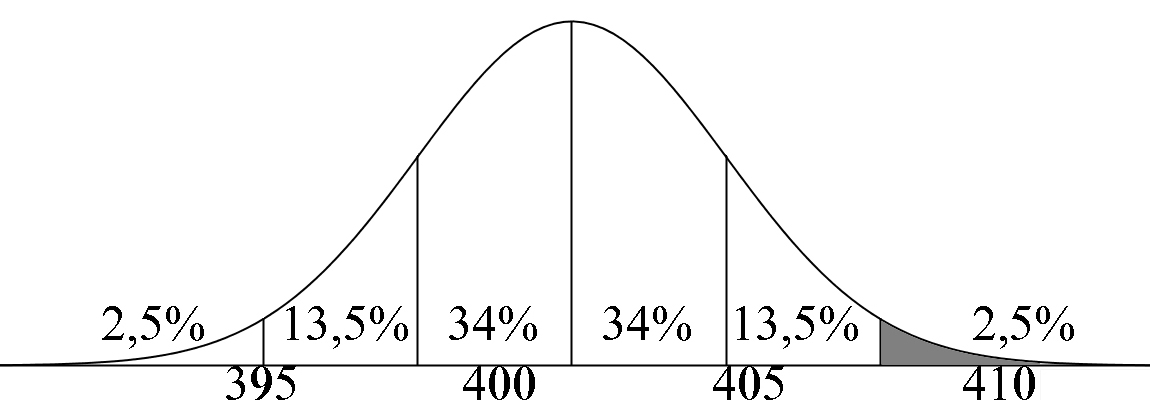
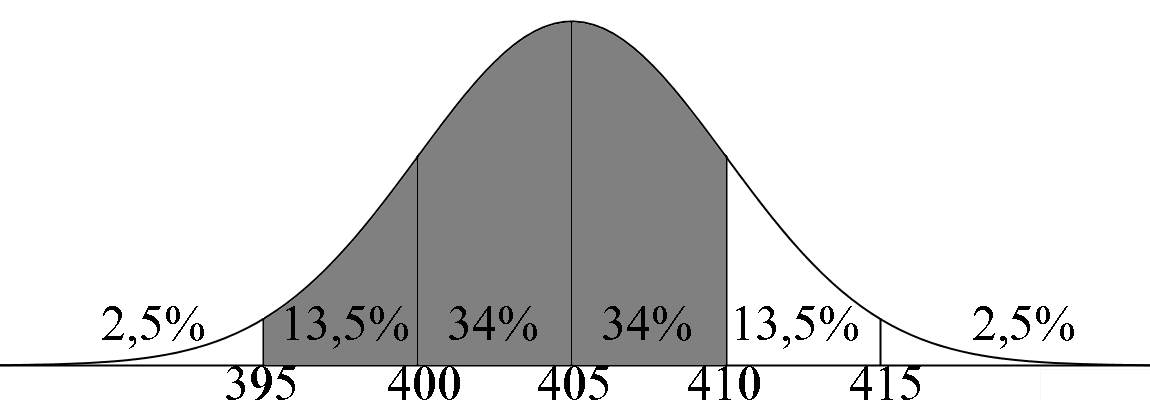
Het gewicht van 1000 pakken hagelslag van Venz is normaal verdeeld met een µ van 405 gram en een σ van 5 gram. Bereken met behulp van de vuistregels voor de normale verdeling: a) Hoeveel pakken hagelslag minder wegen dan 400 gram b) Hoeveel pakken hagelslag meer wegen dan 415 gram c) Hoeveel pakken er tussen de 395 en 410 gram wegen |
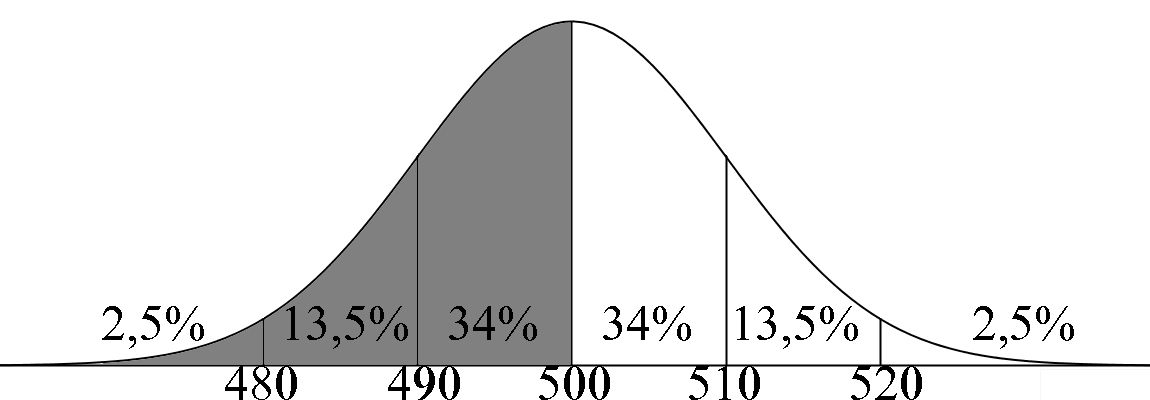
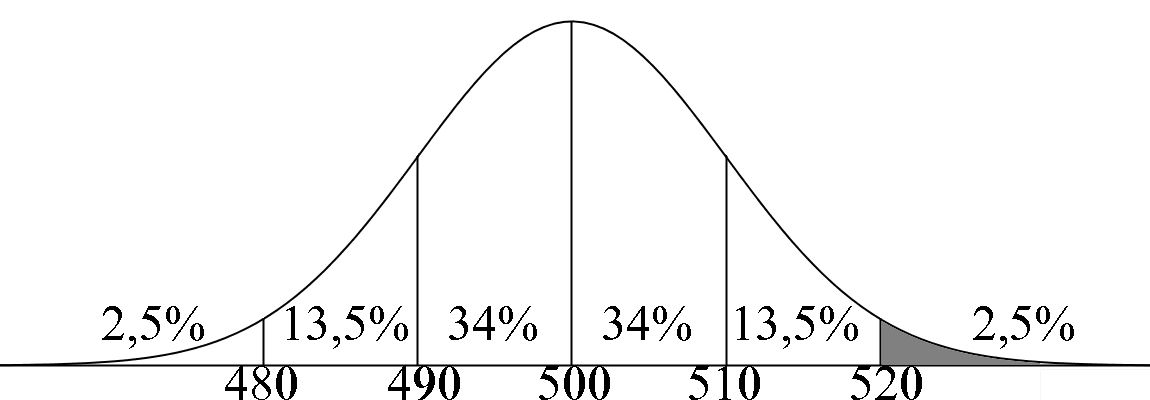
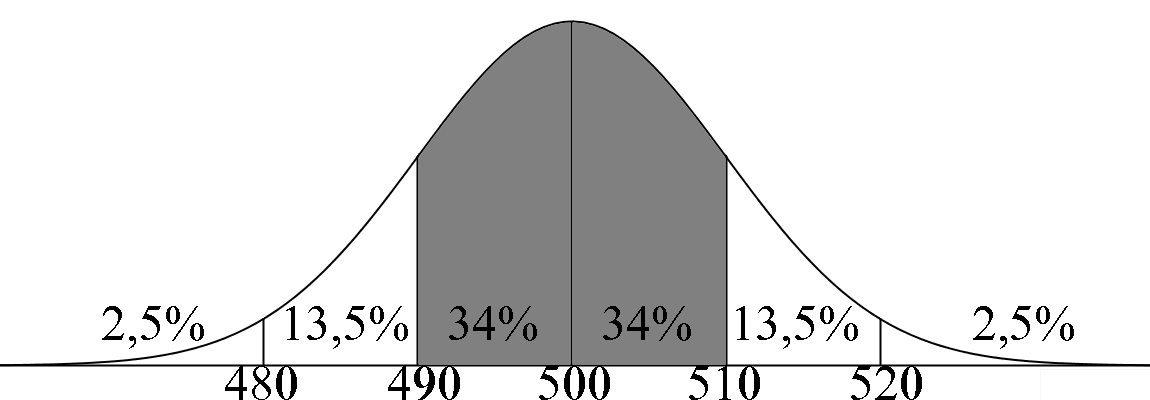
De inhoud van de blikjes Monster bij de Dekamarkt is normaal verdeeld met een gemiddelde van 500 ml en een standaardafwijking van 10 ml. 4HAVO koopt 40 blikjes. Bereken met behulp van de vuistregels voor de normale verdeling: a) Hoeveel blikjes minder dan 500 ml bevatten b) Hoeveel blikjes meer dan 520 ml bevatten c) Hoeveel blikjes er tussen 490 en de 510 ml bevatten |
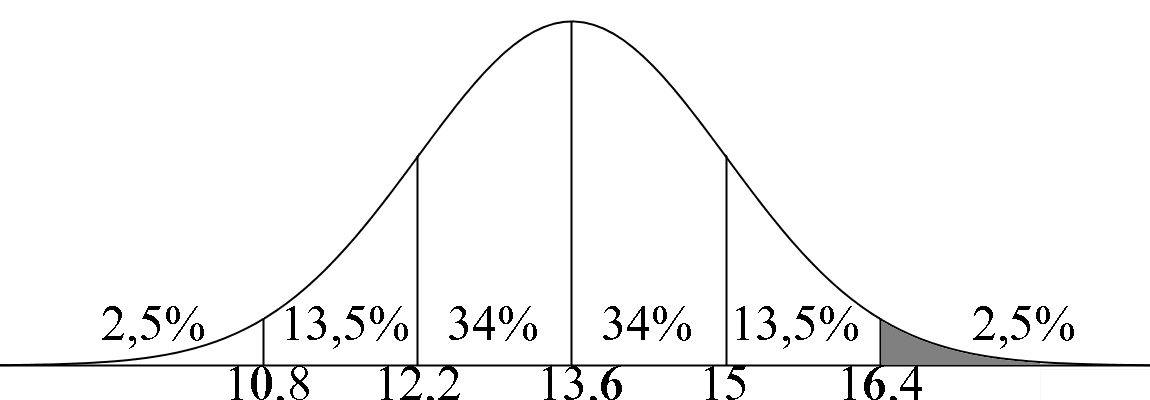
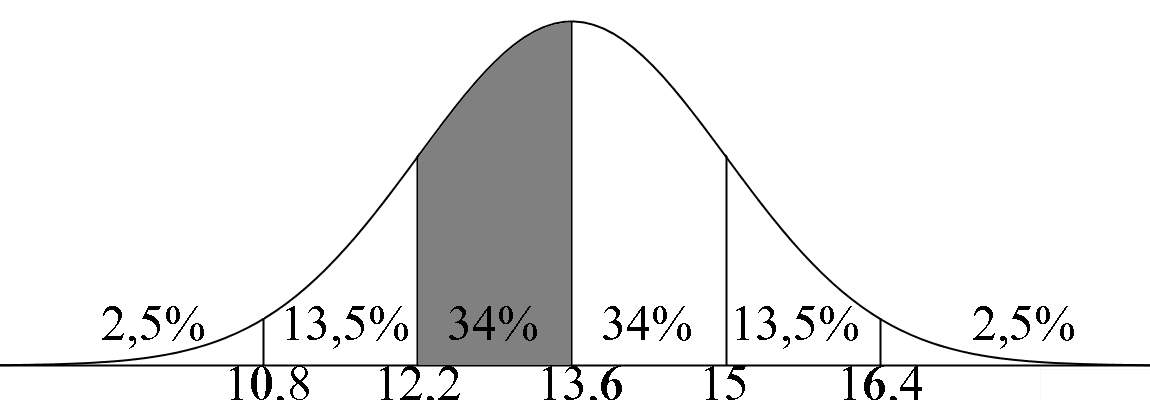
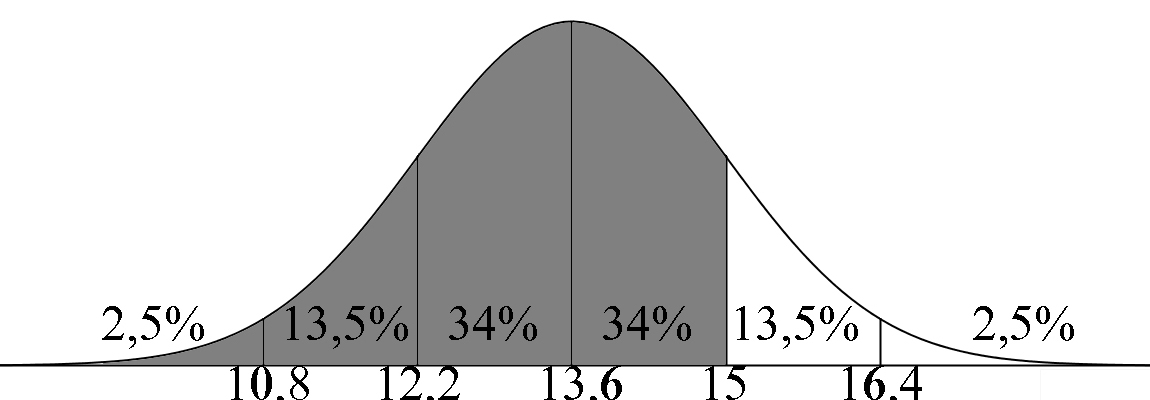
De bladeren van de bomen op het schoolplein van het Bonaventuracollege Burggravenlaan hebben een gemiddelde lengte van 13,6 cm. De lengte is normaal verdeeld met een standaardafwijking van 1,4 cm. Bereken met behulp van de vuistregels voor de normale verdeling: a) Hoeveel procent van de bladeren groter zijn dan 16,4 cm b) Hoeveel procent van de bladeren tussen de 12,2 en de 13,6 cm zijn c) Hoeveel procent van de bladeren kleiner zijn dan 15 cm |
| Antwoorden | ||
 |
 |
 |
|
a) Aflezen: 16% 0,16 * 1000 pakken = 160 pakken |
a) Aflezen: 50% 0,5 * 40 blikjes = 20 blikjes |
a) Aflezen: 2,5% |
 |
 |
 |
|
b) Aflezen: 2,5% 0,025 * 1000 pakken = 25 pakken |
b) Aflezen: 2,5% 0,025 * 40 blikjes = 1 blikje |
b) Aflezen: 34% |
 |
 |
 |
|
c) Aflezen: 81,5% 0,815 * 1000 pakken = 815 pakken |
c) Aflezen: 68% 0,68* 40 blikjes = 27,2 dus 27 blikjes |
c) Aflezen: 84% |
Normale verdeling met de grafische rekenmachine
Onthoud goed:
De oppervlakte onder de hele kromme is altijd 1
De kromme is symmetrisch (je kan hem spiegelen in de lijn ¨¬)
2ND → VARS → 3:invNorm(
2ND → VARS → 2:normalcdf(
Bij alle vragen over een normale verdeling waar de bijbehorende kromme niet gegeven is, moet je hem ZELF tekenen.
1) Normaalkromme tekenen
2) Streep zetten bij de linker- en/of rechtergrens
3) De oppervlakte die je hebt gekregen of moet uitrekenen, inkleuren of arceren
4) Rechtsboven de normaalkromme zetten: µ, σ en opp.
Grens uitrekenen:
invNorm(oppervlakte LINKS naast grens, µ, σ) = grens
Grenzen altijd afronden op 1 decimaal meer dan de gegeven σ, tenzij anders vermeld in de vraag.
| Voorbeelden van vragen | ||
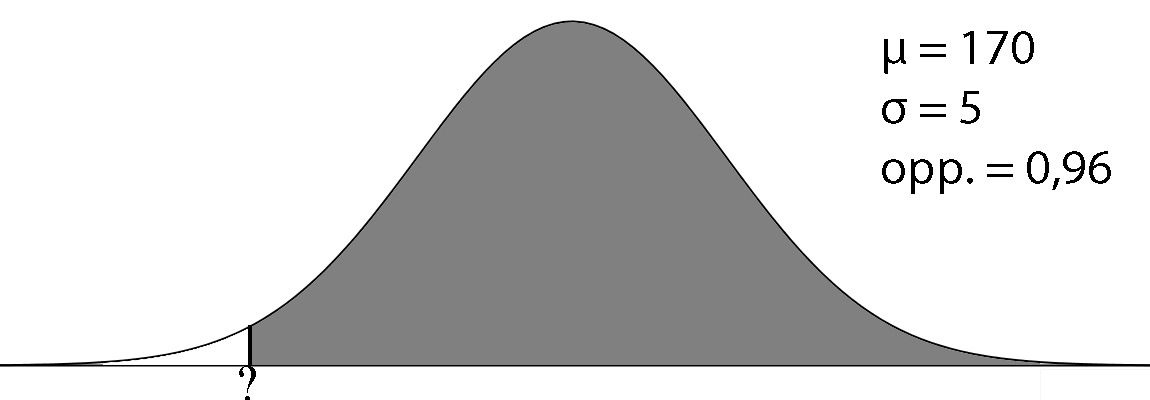
| De lengte van leerlingen in 5VWO is normaal verdeeld met een gemiddelde van 1.70 m en een standaardafwijking van 5 cm. Het blijkt dat 96 procent van de leerlingen zonder op een stoel of een krukje te gaan staan, spullen van de kasten in de wiskundelokalen kan pakken. Mevrouw Wolleswinkel was in 5VWO (en is nu nog steeds) 1.60 m, laat met een berekening zien of zij zonder een stoel of krukje iets van de kasten in de wiskundelokalen pakken. | De scores van 20.000 kinderen op de intelligentietest Wechsler Intelligence Scale for Children (WISC) zijn bij benadering normaal verdeeld met gemiddelde 100 en standaardafwijking 15. De 3% slimste kinderen van deze groep worden uitgenodigd voor een honours class. Vanaf welke score word een kind uitgenodigd? Rond af op gehelen. | Omdat het de afgelopen tijd warmer was dan normaal rond deze tijd van het jaar, worden op een fruitveiling 10% meer aardbeien aangeleverd dan er gevraagd worden. Om te zorgen dat de aardbeiprijs niet instort besluit de veilingdirectie in overleg met de kwekers dat de 5% grootste en de 5% kleinste aardbeien niet verkocht worden. Er wordt een steekproef gedaan en daaruit blijkt dat de aarbeien gemiddeld 4 cm zijn met een standaardafwijking van 0,5 cm. welke groottes van aardbeien worden er op de veiling verkocht? Rond af op 2 decimalen. |
| Antwoorden | ||
 |
 |
 |
|
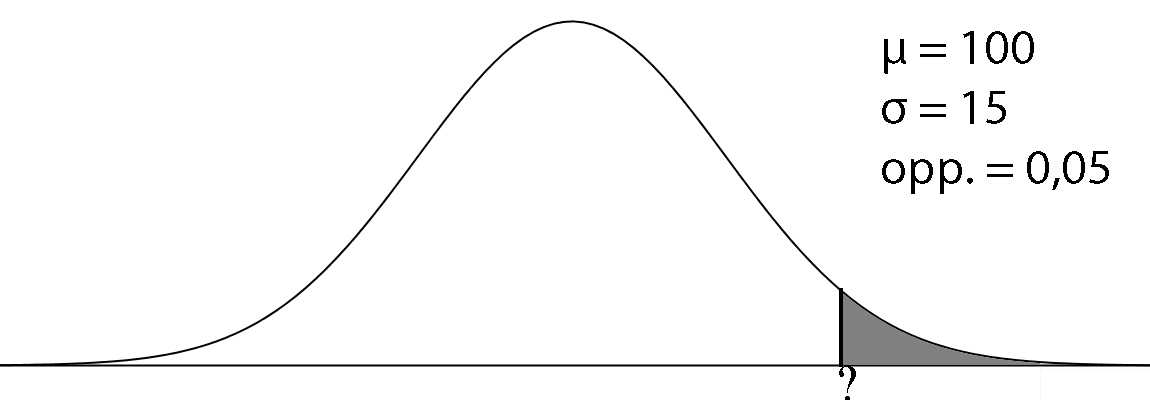
Let op! Alles in dezelfde eenheden zetten! µ = 170 cm en σ = 5 cm OF µ = 1,70 m en σ = 0,05 m Let op! Bij invNorm ltijd de LINKER oppervlakte pakken. Opp. links = 1 - 0,96 = 0,04. grens = invNorm(0.04, 170, 5) = 161,3 cm OF grens = invNorm(0.04, 1.70, 0.05) = 1,613 m Iedereen onder de 1,613 m is te klein. Mevrouw Wolleswinkel zal dus een stoel of een krukje moeten pakken. |
Let op! Bij invNorm altijd de LINKER oppervlakte pakken. Opp. links = 1 - 0,03 = 0,97. grens = invNorm(0.97, 100, 15) = 128,2 Kinderen met een score van 128 hebben net een te lage score. Vanaf 129 worden kinderen uitgenodigd. |
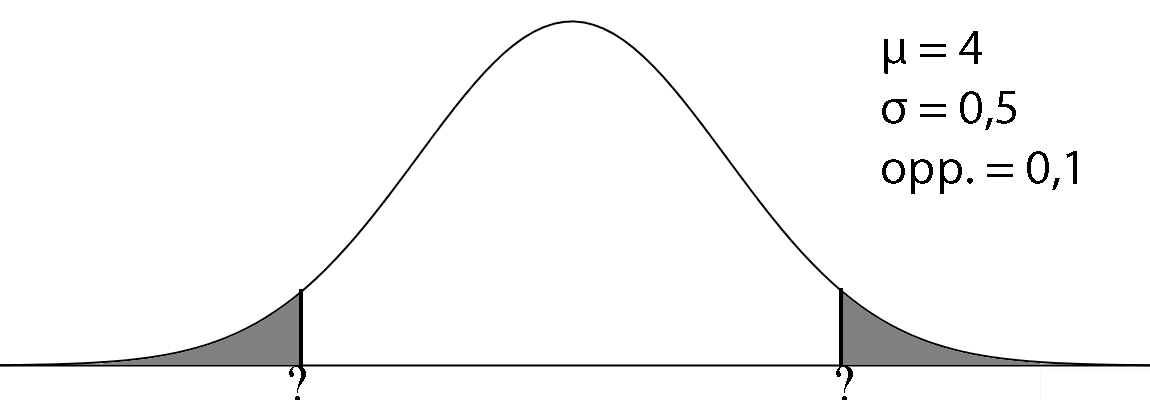
Hier wordt om twee waarden gevraagd. grens1 = invNorm(0.05, 4, 0.5) = 3,18 cm Aardbeien van 3,17 worden nog teruggestuurd, vanaf 3,18 worden ze geveild. Let op! Bij invNorm altijd de LINKER oppervlakte pakken. Opp. links = 1 - 0,05 = 0,95. grens2 = invNorm(0.95, 4, 0.5) = 4,82 cm Aardbeien van 4,82 worden nog geveild, vanaf 4,83 worden ze teruggestuurd. Aardbeien vanaf 3,18 cm tot en met 4,82 cm worden geveild. |
Oppervlakte uitrekenen:
normalcdf(linkergrens, rechtergrens, µ, σ) = oppervlakte
| Voorbeelden van vragen | ||
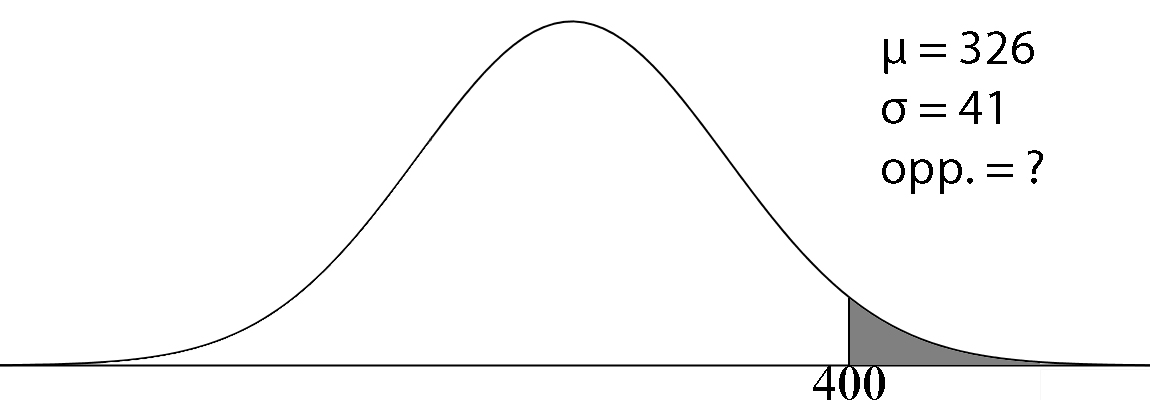
| Een van de eerste dagen van de herfstvakantie is de wachttijd voor de pashokjes van de Primark in Rotterdam normaal verdeeld met een gemiddelde 20 minuten en een standaardafwijking van 10 minuten. Je moet na het shoppen je trein halen, je kunt dus echt niet langer dan een kwartier wachten. Hoe groot is de kans dat je in een pashokje kunt passen? | Je koopt een nieuwe smartphone, het blijkt dat de levensduur van de gemiddelde smartphone 7,1 jaar is, met een standaardafwijking van 2,3 jaar. Hoe groot is de kans dat je smartphone binnen twee jaar stuk is? | Het aantal 10 euro biljetten dat per dag uit de ING automaat op de Haarlemmerstraat wordt gehaald is gemiddeld 326 met een standaardafwijking van 41. De geldautomaat wordt dagelijks aangevuld tot 400 biljetten van 10 euro. Het kan natuurlijk gebeuren dat alle biljetten van 10 euro op zijn voordat de automaat weer wordt aangevuld. Bereken op hoeveel dagen van een jaar dat naar verwachting zal gebeuren. |
| Antwoorden | ||
 |
 |
 |
|
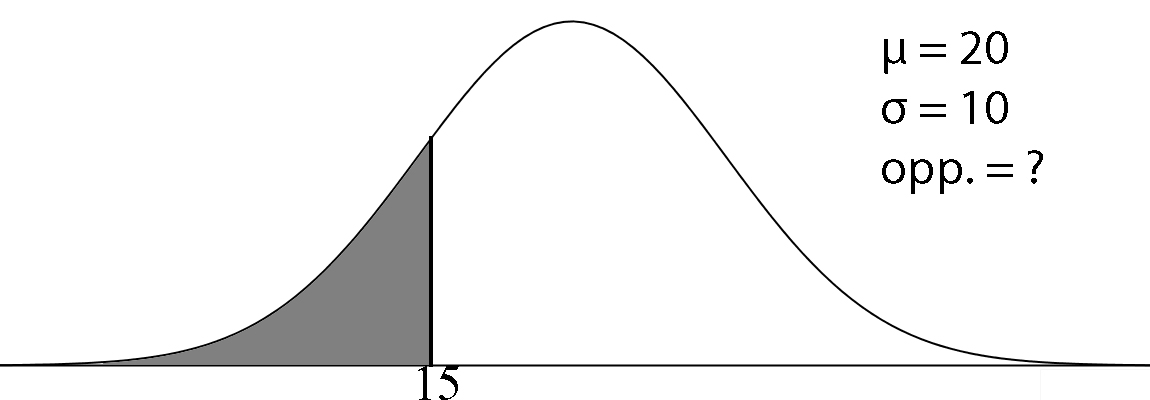
Je moet de kans uitrekenen dat je 15 minuten of minder moet wachten. normalcdf(-1099, 15, 20, 10) = 0,309 De kans dat je kunt passen in een pashokje is 0,309. |
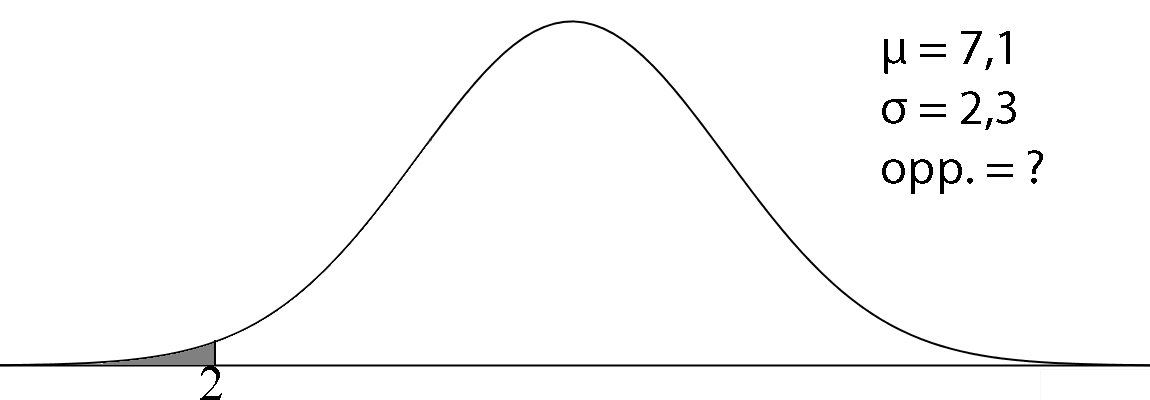
normalcdf(-1099, 2, 7.1, 2.3) = 0,013 De kans dat je telefoon binnen twee jaar stuk is, is 0,013. |
Je moet eerst de kans uitrekenen dat er op een dag 400 of meer briefjes uit de automaat worden gehaald. normalcdf(400, 1099, 326, 41) = 0,0355 0,0355 * 365 = 13 dagen. |
µ uitrekenen:
Y1 = normalcdf(linkergrens, rechtergrens, X, σ)
Y2 = oppervlakte
Optie intersect geeft x = ... en y = ...
Dus: µ = ... (de waarde die je voor x hebt gevonden)
OF
Y1 = invNorm(oppervlakte LINKS naast grens, X, σ)
Y2 = grens
Optie intersect geeft x = ... en y = ...
Dus: µ = ... (de waarde die je voor x hebt gevonden)
| Voorbeelden van vragen | ||
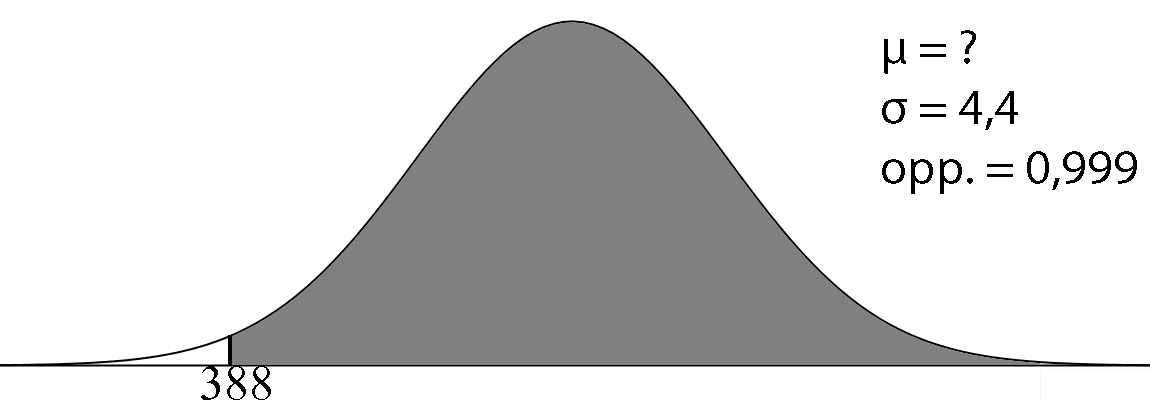
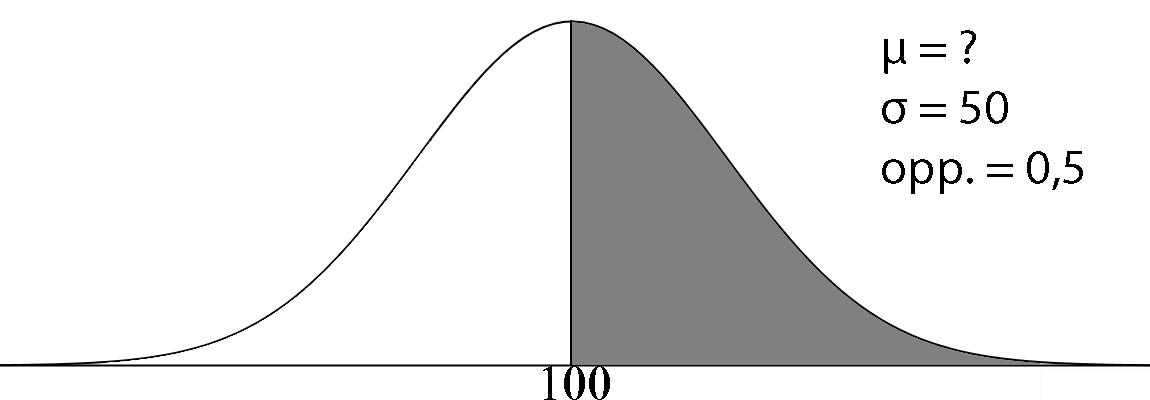
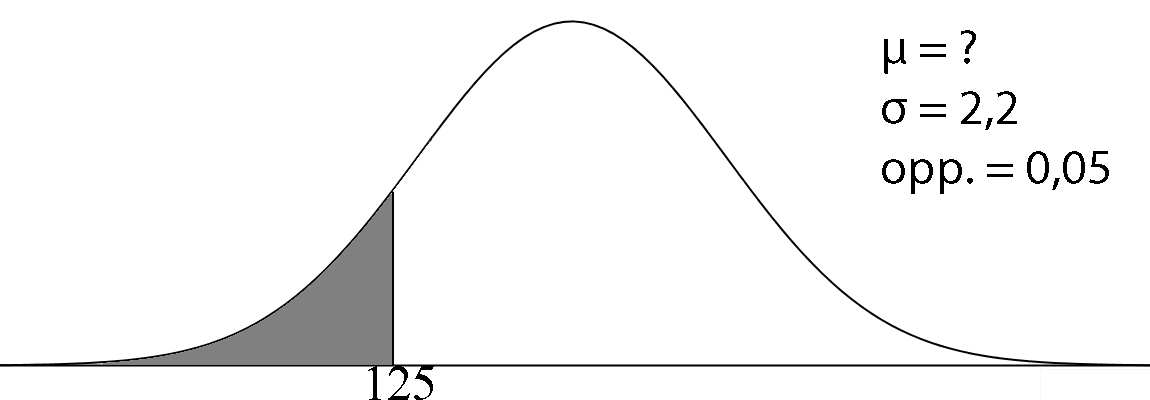
| Op een pot chocopasta van Nutella staat: inhoud: 400 gram e. Dat betekent dat er minstens 388 gram in ieder potje moet zitten. Nutella houdt niet zo van boetes, dus ze willen ervoor zorgen dat 99,9% van alle potten die uit de fabriek komen, aan de norm voldoen. Ze hebben een vulmachine staan die altijd een standaardafwijking van 4,4 gram heeft. Op hoeveel gram moet Nutella de vulmachine afstellen? Rond je antwoord af op gehelen. | Een aantal scholieren nemen voor hun profielwerktstuk een enquete af. Ze doen dat door hun vragen naar hun hele MSNlijst te sturen. Het blijkt dat de standaarddeviatie van het aantal mensen dat in de MSNlijsten staat, 50 is. De helft van de leerlingen krijgt meer dan 100 reacties. Hoeveel mensen hebben de leerlingen gemiddeld in hun MSNlijst? | Het bedrijf OLA verkoopt 2,94 miljoen kleine bekertjes met roomijs. Op de bekertjes staat dat er 125 ml in zit. De machine die de bekertjes vult is ingesteld op 129,8 ml en heeft een standaardafwijking van 2,2 ml. De overheid eist dat hooguit 5% van de bekertjes minder dan 125 ml ijs bevat. OLA kan zijn vulgemiddelde lager instellen, en toch aan de eis van de overheid voldoen. De standaardafwijking van de machine verandert nooit. Omdat OLA zoveel ijs verkoopt, levert een lager vulgemiddelde een aardige besparing op van de hoeveelheid roomijs die geproduceerd moet worden. De productiekosten van roomijs zijn 0,73 euro per liter. Bereken hoeveel euro OLA maximaal kan besparen. |
| Antwoorden | ||
 |
 |
 |
|
Let op! Voor invNorm altijd de oppervlakte LINKS nemen. Opp. links = 1 - 0,999 = 0,001 invNorm(0.001, ?, 4.4) = 388 Y1 = invNorm(0.001, X, 4.4) Y2 = 388 Optie intersect geeft x = 401,597 en y = 388 Bij 401 gram komt er nog te weinig pasta in de potjes. Nutella moet zijn machine afstellen op 402 gram. OF normalcdf(388, 1099, ?, 4.4) = 0,999 Y1 = normalcdf(388, 1099, X, 4,4) Y2 = 0,999 Optie intersect geeft x = 401,597 en y = 0,999 Bij 401 gram komt er nog te weinig pasta in de potjes. Nutella moet zijn machine afstellen op 402 gram. |
Let op! Voor invNorm altijd de oppervlakte LINKS nemen. Opp. links = 1 - 0,5 = 0,5 invNorm(0.5, ?, 50) = 100 Y1 = invNorm(0.5, X, 50) Y2 = 100 Optie intersect geeft x = 100 en y = 100 Leerlingen hebben gemiddeld 100 mensen in hun MSNlijst. OF normalcdf(100, 1099, ?, 50) = 0,5 Y1 = normalcdf(100, 1099, X, 0.5) Y2 = 0,5 Optie intersect geeft x = 100 en y = 0,5 Leerlingen hebben gemiddeld 100 mensen in hun MSNlijst. |
invNorm(0.05, ?, 2.2) = 125 Y1 = invNorm(0.05, X, 2.2) Y2 = 125 Optie intersect geeft x = 128,619 en y = 125 Dus: µ = 128,6 (de machine wordt ingesteld op 1 decimaal, zie vraag). OF normalcdf(-1099, 125, ?, 2.2) = 0,05 Y1 = normalcdf(-1099, 125, X, 2.2) Y2 = 0,05 Optie intersect geeft x = 128,619 en y = 0,05 Dus: µ = 128,6 (de machine wordt ingesteld op 1 decimaal, zie vraag). 129,8 - 128,6 = 1,2 ml per bakje roomijs wordt bespaard. 1,2 ml * 2,94 miljoen = 3,528 miljoen ml roomijs = 3528 liter roomijs 3528 * 0,73 = 2575 euro. Een besparing van 2575 euro. |
σ uitrekenen:
Y1 = normalcdf(linkergrens, rechtergrens, µ, X)
Y2 = oppervlakte
Optie intersect geeft x = ... en y = ...
Dus: σ = ... (de waarde die je voor x hebt gevonden)
OF
Y1 = invNorm(oppervlakte LINKS naast grens, µ, X)
Y2 = grens
Optie intersect geeft x = ... en y = ...
Dus: σ = ... (de waarde die je voor x hebt gevonden)
| Voorbeelden van vragen | ||
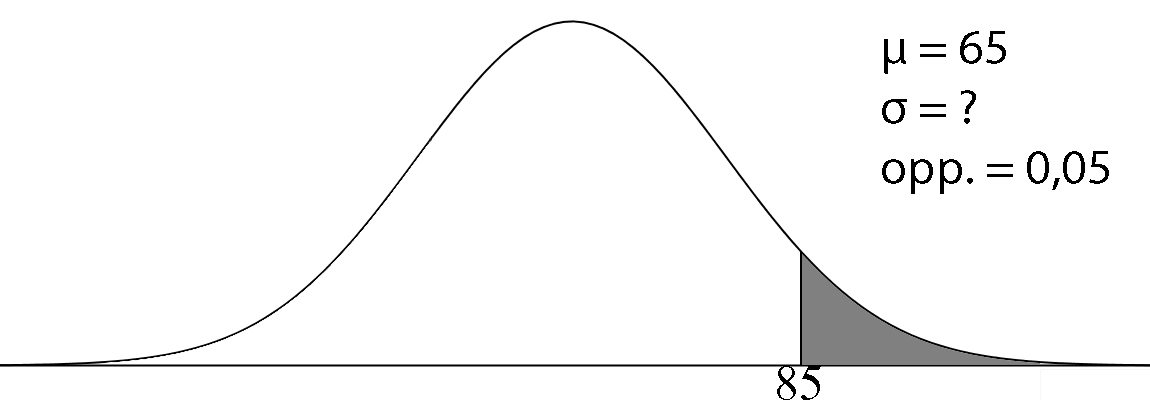
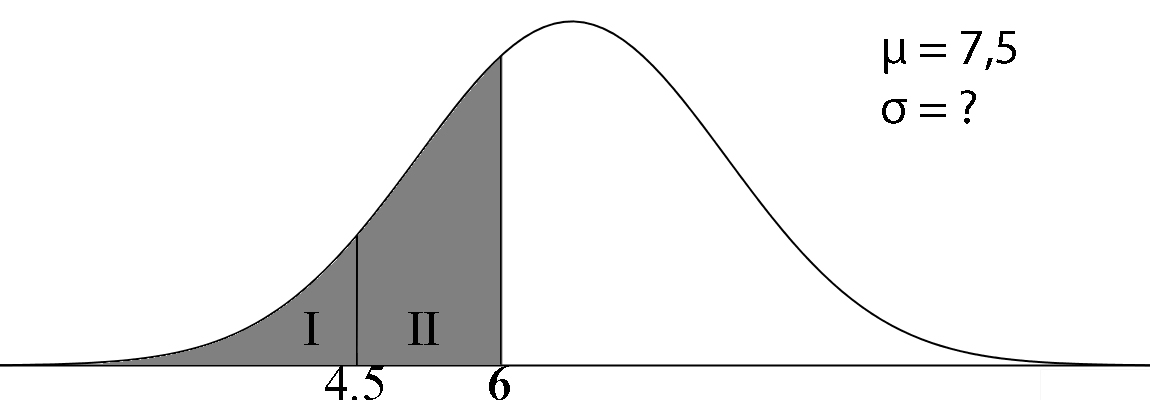
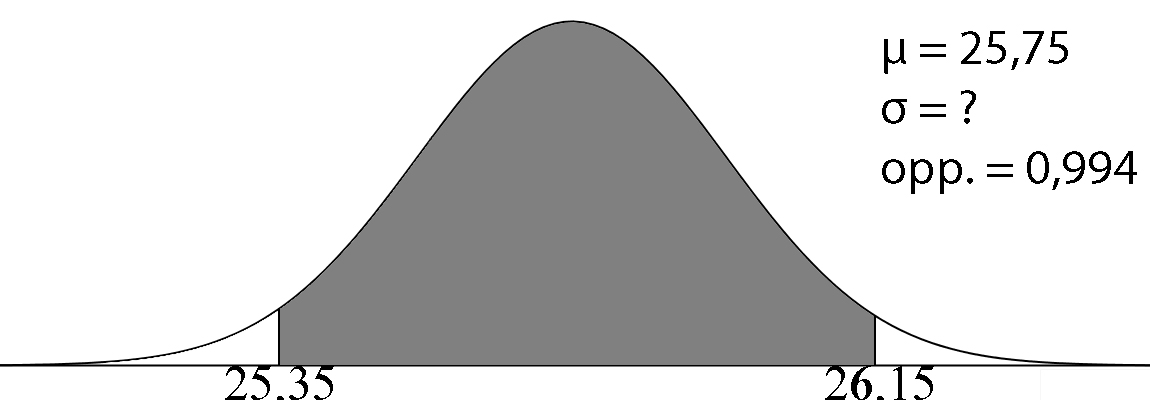
| De 500 leden van een hockeyclub worden vijf jaar lang in de gaten gehouden. Alle leden worden op verschillende aspecten getest en krijgen een score van 0 tot 100 die aangeeft hoe goed hij of zij is. Gemiddeld scoorden de leden 65. Ervaring leert dat de beste 5% van de leden binnen 5 jaar overstapt naar een andere vereniging. Alle leden met een score van 85 en hoger blijken na 5 jaar overgestapt te zijn. Bereken de bijbehorende standaarddeviatie. | Uit onderzoek blijkt dat jongens uit de eerste klas gemiddeld 7,5 uur aan hun huiswerk besteden. Een wetenschapper doet onderzoek naar eersteklas jongens die minder dan 6 uur aan hun huiswerk besteden. Hij schrijft op hoeveel uur ze precies aan hun huiswerk besteden. De mediaan van zijn meetwaarden is 4,5 uur. Bereken de bijbehorende standaardafwijking. | De snoepautomaat in de aula is zo nauwkeurig afgesteld, dat een munt van 2 euro wordt geweigerd als hij meer dan 0,40 mm afwijkt van het gemiddelde. De gemiddelde diamenter van een twee euro munt is 25,75 mm. In de automaat worden in de loop van de tijd 1000 twee euro munten gedaan. De automaat weigert 3 munten omdat ze te klein zijn en 3 munten omdat ze te groot zijn. Bereken de standaardafwijking van de diameter van de twee euro munt in 2 decimalen. |
| Antwoorden | ||
 |
 |
 |
|
Let op! Voor invNorm altijd de oppervlakte LINKS nemen. Opp. links = 1 - 0,05 = 0,95 Y1 = invNorm(0.95, 65, X) Y2 = 85 Optie intersect geeft x = 12,159 en y = 85 Dus: σ = 12 OF Y1 = normalcdf(85, 1099, 65, X) Y2 = 0,05 Optie intersect geeft x = 12,159 en y = 0,05 Dus: σ = 12 |
Mediaan dus oppervlakte I = opppervlakte II opp. I = normalcdf(4.5, 6, 7.5, ?) opp. II = normalcdf(-1099, 4.5, 7.5, ?) Y1 = normalcdf(4.5, 6, 7.5, X) Y2 = normalcdf(-1099, 4.5, 7.5, X) Optie intersect geeft x = 2,915 en y = 0,152 Dus: σ = 2,915 uur |
Let op! Voor invNorm altijd de oppervlakte LINKS nemen. Opp. links = 0,003 Y1 = invNorm(0.003, 25,75, X) Y2 = 23,35 Optie intersect geeft x = 0,1456 en y = 23,35 Dus: σ = 0,15 mm OF Y1 = normalcdf(25.35, 26.15, 25.75, X) Y2 = 0,994 Optie intersect geeft x = 0,1456 en y = 0,994 Dus: σ = 0,15 mm |

